Patrik Ferrari
Research activityThe main focus in my research activity is the question of universality of fluctuations under appropriate scaling limits. The probabilistic models which we study are often, but not exclusively, motivated by statistical mechanics in and out of equilibrium. Here are some of these models, some of them being tightly related, others having only connections after taking the scaling limits. On the right, a snapshot of a 2+1 dimensional growth model studied in this paper: the projection to fixed time leads to a random tiling model, while the projection to a lower space dimension is a 1+1 growth models in the KPZ universality class.
| 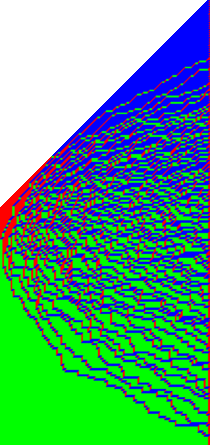 |
Below you can find animation of (some of) these models.
Javascript Animations
See W3Schools for a good guide.
| • | A growth model in the 2+1 dimensional anisotropic KPZ class | Javascript |
| • | The totally asymmetric simple exclusion process (TASEP) | Javascript |
Animations
Java applets do not generically run anymore within internet browers. They can still be run if you install the program appletviewer. Be aware that you need to have installed also the JDK in a version before 9.
| • | The continuous time polynuclear growth (PNG) model | Java Applet |
| • | The totally asymmetric simple exclusion process (TASEP) | Java Applet |
| • | A growth model in the 2+1 dimensional anisotropic KPZ class | Java Applet |
| • | A 2+1 dimensional particle dynamics and the Aztec diamond | Java Applet |
| • | A visualization of the slow decorrelation phenomena | Java Applet |
| • | A visualization of the qTASEP | Java Applet |
| • | A visualization of GOE-GOE shock in TASEP | Java Applet |


